Bakı Dövlət Universiteti Rəqəmsal Tədqiqat Laboratoriyası

Xülasə:

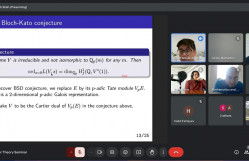
One of the central problems in number theory is the Birch and Swinnerton-Dyer conjecture, which asserts that the order of vanishing of the L-function of a rational elliptic curve E at the central value coincides with the rank of its Mordell-Weil group. A far-reaching generalization of this is the Bloch-Kato conjecture, which posits a similar relationship between the order of vanishing of the L-functions associated with Galois representations and the dimension of their Selmer groups. In recent years, significant progress has been made in establishing new cases of this conjecture for automorphic Galois representations arising in the cohomology of Shimura varieties, most notably in the work of Skinner, Loeffler, and Zerbes for GSp4-Shimura varieties. A crucial ingredient in these developments is the construction of an Euler system, a powerful tool for studying the dimension of Selmer groups.

In this talk, we recall the Bloch-Kato conjecture in the setting of GSp6-Shimura varieties and present the construction of an Euler system using a novel method that overcomes a major obstacle. As a consequence, we obtain the first non-trivial result towards the Bloch-Kato conjecture in this setting.